The Airplane on a Treadmill

The problem is as follows:

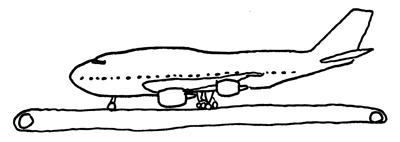
Suppose that there is an airplane on a treadmill, a treadmill as long and wide as a runway. The treadmill is designed such that its speed exactly matches the speed of the airplane's wheels, but moving in the opposite direction. Can the plane take off?

It's a neat question, if only for the visual of a 747 on a treadmill, its turboprops amounting to the world's largest hair dryers as the treadmill hums underneath madly spinning landing gear. And it's certainly true that a treadmill could push a plane backwards hard enough that it could fully oppose the thrust from the plane's engines.

Typical approaches toward this problem have been mathematical and focused on defining the velocity of the treadmill itself. However, I don't think that's the right tack. The question is deceptively formulated and conceals the issue at the heart of this problem: not velocity, but acceleration. We can assume that the plane has a velocity below escape velocity, else it would already be airborne. Moreover, whether it begins at 0mph or somewhere in the middle isn't important in principle - the goal of the plane, whatever its initial velocity, is to accelerate to the velocity at which its wheels leave the green earth. The goal of the treadmill, therefore, is to prevent any acceleration, as with a non-zero acceleration the plane will eventually reach escape velocity. Or more realistically, with a non-zero acceleration the question turns into an engineering problem: are the plane's engines strong enough to accelerate it quickly enough to reach escape velocity, even when opposed by the treadmill?¹

So, the question becomes: can the treadmill prevent the plane from accelerating, by adjusting to the plane's velocity?

And the answer is no, it can't. In order for the treadmill to prevent the plane's speed from changing, the treadmill must be able to speed up itself. But the treadmill's speed is tied directly to the plane's wheels speed. Therefore, in order to speed up it must detect a change in the plane's velocity. IE, in order for the treadmill to speed up, the plane itself must first speed up. The plane has therefore a non-zero acceleration, and eventually takes off. Moreover, the treadmill can't keep the plane from accelerating even by adjusting for the plane's acceleration, for it would not be able to prevent a change in acceleration, or, jerk. You could keep rolling down that chain of derivatives forever, becoming perhaps more efficient but never truly keeping that plane on the ground. This is because these systems - adjusting for impulse change in velocity and adjusting for impulse change in acceleration - are identical in concept. An impulse change in velocity is a discontinuous function, which means that not only would you change the function itself, but you change all of its derivatives. Therefore, speed, acceleration, jerk, etc. are all the same thing here. And given a long enough treadmill (or a short enough treadmill ¹) the plane can not be prevented from accelerating. Its acceleration may only be incompletely opposed.

The issue at the heart is that one can not prevent change by reacting to change, and one can not negate change by correcting to the change instead of correcting for the change. I could put it to you another way: suppose that the devil has a glass of ice water he wants to save for dinner, and he charges one of his demons to keep the ice from melting. The demon, being a little behind the curve, puts the ice water in the freezer whenever he sees some ice melt, but fearing the devil's wrath should the glass of water freeze solid, he removes the glass shortly after putting it in. He's a very fast demon, perhaps, and reacts quickly to the smallest melting. But the demon's task is impossible, for the change he is trying to prevent is a change he may only react to, and not a change he can correct for.

The only way to hold the plane down would be to adjust the treadmill's speed (and thereby, the acceleration due to the frictional force on the landing gear) in concert with the thrust produced by the plane's engines. But then the question - if a plane's thrusters are perfectly opposed by some other force, can it take off? - is really dumb.


Hat tip to the XCKD blag, which gave me this idea and that awesome picture in the first place.




1 Actually, if the plane accelerates at all it will eventually leave the treadmill. Since the treadmill is of finite length (as long and wide as a runway,) if the plane moves at all with respect to the treadmill it's good as in the sky. Well, unless the treadmill was constructed at LaGuardia.