Recently, I was playing Monopoly with my darling wife. The first game, I got lucky and bought all four railroads and the orange set of properties. I leveraged everything for hotels and won that game handily. But the second game brought the nightmare scenario: all properties purchased, no monopolies.
Rather than restart the game, we began bargaining. I resolved to hold firm until I got a deal that favored my cause - don't look at me like that, she's more competitive than I - and rejected a couple of her trades right off the bat. But then, she offered me one I couldn't pass up. I had two out of three green squares (heretofore my favorite properties) and two out of three red squares. She had two out of three yellow squares. Her proposal: trade her the last yellow property and one of the reds for the last green. I eagerly accepted, again mortgaged everything to buy houses... and got completely hosed. I looked at her yellow properties - three hotels - and looked at my greens, with three or four houses apiece. Needless to say, successfully running that gauntlet was never going to happen.
 Now this was remarkable - the orange properties clearly annihilated the a block of properties three full blocks ahead of them. Clearly, there was some hidden pattern that one could exploit in a trade. Of course, my nerd-sense was piqued. "I can feel an Excel spreadsheet coming on..." I said. She just shook her head.
Now this was remarkable - the orange properties clearly annihilated the a block of properties three full blocks ahead of them. Clearly, there was some hidden pattern that one could exploit in a trade. Of course, my nerd-sense was piqued. "I can feel an Excel spreadsheet coming on..." I said. She just shook her head.BTW: I'm just a single nerd. Any nerds who want to CMIIW, well, I'll buy you a Coke.
Here's the board in question:

Property cost increases in a fairly continuous manner as one travels around the board. If we exclude the purples and the dark blues, cost of property begins at $100 and increases by $20 every time the last or first property in a block is reached. Likewise, house cost increases stepwise by $50, with the first flight of properties requiring $50 per house, the second requiring $100, the third requiring $150, and the fourth requiring $200.

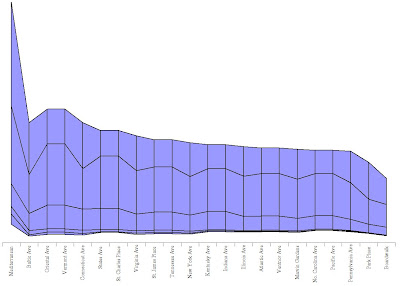
Taking them together, we can plot the cost of attaining the different states (0 houses, 1 house, 2 houses...) for each property:

One can already see that the two twin-property blocks (purples and dark blues) don't fit the trend - they are simply too cheap to develop because you only have to buy two of them to start building houses. This is obvious, of course. What I hadn't expected was that price would peak at the green properties - Boardwalk and Park Place require a slightly larger initial investment per-property, but are still cheaper to develop than their preceding neighbors. The green properties are the most expensive to develop on the entire board.
Rent increases in a continuous yet idiosyncratic manner:

Trends are less illuminating here. We notice the gradual increase from left-to-right, and the fact that no single property charges less rent than any property before it. But other than that, there doesn't seem to be any unifying trend. The behavior in the mauve block is particularly weird, and again, the twin-property blocks are outliers.
But how do those trends interact? Monopoly's nut and bolts are proper investment - therefore, one should form a trading strategy that maximizes return on investment. Of course it's true that merely breaking even on a property does not mean you've bankrupted your opponent. However, breaking even does mean that you've spent less money on that property than your opponent - the soul of good development. So I figured one could roughly model a property's success rate by calculating the probability that the greedy landlord will recoup their initial ante.
First, we must calculate the ratio of rent to investment. For a single, naked property, that would be the rent you collect divided by the purchase cost of that property:
and for a property with houses:
This number shows us how much money one gets in rent as a percentage of the money you invested into the property - the efficiency of investment. I calculated this number for all states of the property (zero houses, one house, two houses, etc.):

A visually-pleasing color-coded version, you say? Voila:

Another trend becomes evident: the first block of properties in a flight is less efficient than the second block. You pay the same for a house in the red block as you do in the yellow block, but you get less rent out of it. Thus, while no property charges less rent than any property before it, some properties charge less rent per dollar invested than some properties before them. IE, they have a lower
From
Pretty simple. The number of times one must land on the property is the number of times that the rent goes into the investment:
This number is useful when we consider the probability of landing on each property. It is conceivably possible to calculate the probability of landing on each property based on its position - I don't know how to do that. Lucky for us, a helpful guy out on the interwebs has done just that:

Note: he's approached the game differently than I. Take that as you will.
He has determined the probabilities based on two different game strategies. The "short" strategy is an early-game strategy in which players pay to get out of jail as quickly as possible, so to buy up property. The "long" strategy is a late-game strategy in which players stay in jail as long as possible, so to avoid paying rent. This strategy increases the probability of being in jail a little less than three-fold, which we would expect - players may stay in jail until they pay, roll doubles, or three turns have passed at which time they must pay $50 and leave. For the regular properties, this means the probability of landing on any property space is somewhat decreased. There are some weirdnesses associated with that, but I'm really not qualified to discuss them.
First, notice the random peaks at Illinois, New York, Boardwalk, and St. Charles. You can be sent to all three of these properties directly by chance cards. New York is a lesser peak because its card is "Go Back Three Spaces" which has different effects based on which of three chance locations you have landed on. You can also be sent to Go, Reading Railroad, or to Jail by cards (or by the Go To Jail square.) All of this tends to weight the front half of the board much more heavily in terms of probability. Essentially, the probability peaks around free parking (though this doesn't explain why I never land on free parking and my wife always does. Go figure.) This shows us that while the earlier properties may not draw as much rent, you do land on them more often.
So how do those two trends (required lands and probability of a single land) interact? Now that we know the probability of landing on each square and we know the required number of landings to recoup investment, it is simple to calculate the probability of breaking even. If a certain event has a probability A, the probability of that event occurring B number of times is A^B. So, the probability of recouping an investment in a single Monopoly property by landing only on that property is:
A graph of that is pretty interesting. Here are two graphs, for "short" and "long" strategies respectively:


First off, I know what everyone is already thinking: Park Place/Boardwalk appear bizarrely awesome, total outliers. Likewise, Mediterranean Avenue and Baltic Avenue appear absolutely worthless. Within the middle eighteen properties, where a strong trading strategy is less immediately intuitive, the function clearly points to a sweet spot around the mauve properties. In particular, it points to the light blue properties - somewhat of a surprise. If Monopoly was the Houston Rockets, then Connecticut Avenue would appear to be Shane Battier.
But that still doesn't tell us everything. After all, one does not buy single properties in Monopoly. One buys streets, the success of which is dependent upon the success of all two or three properties therein. Calculating the successfulness of each block is a little trickier. If you're a math geek and I've made an error somewhere, step in. Here's my approach. What we need first is the rent which we are likely to be charged if we land within a certain block. This is not the simple arithmetic mean of the rents being charged on all three properties. If Baltic charges $1,000 and Mediterranean charges $1, the arithmetic mean is $500.50. But if Baltic gets a land 1% of the time and Mediterranean gets the remaining 99%, the true likely rent value is much closer to $1. We really need to model the land as two events: landing on a certain block, and landing on a particular square within the block. The process is akin to a current divider, or partial pressures in chemistry. If a player lands within a certain block, the probability he will land on a certain square is the independent probability of landing on that square divided by the probability of landing on any square in that block (the sum of the probabilities.) We can then multiply the resultant probabilities by their corresponding rents, and add these together to get a probability-adjusted rent for the entire block:
And the graph thereof:= probability of landing on a particular property (n) in the block
= probability of landing on one of those properties (IE, sum of the probabilities)
= the rent charged by that property (n) with a certain number of houses (h)

Note: in this calculation I've assumed that all three properties would have the same number of houses. I may have some time on my hands, but I don't have the kind of time I'd need to calculate all 4,032 combinations.
Investment, likewise, was calculated by summing the costs of all three properties, plus the cost of all the houses:

Rent/investment ratio is calculated as before, but with the adjusted values:

And of course, the charismatic colored version:

And again we graph the reciprocal, which shows us the number of lands necessary to recoup investment. Nothing new here, there is an abrupt dip at the orange block:

Broadway's grip is slowly weakening...
For the calculation of whole-block probabilites, the value used for probability is the sum of the probabilities of the squares within each block. Compared to the earlier graph of probability (which is somewhat of a mess) this one is exceedingly clear. Probability peaks somewhere around free parking:

Using these recalculated values, probability of recouping investment is calculated as before
...giving us this graph:


And it's rather profound. The orange properties are easily the best on the board - even better than the vaunted Broadway and Park Place. And my beloved green properties? Nasty, nasty bad. The maximum probability of recouping your investment on the greens is 0.0004, or 1 in 2500. Comparatively, the maximum for the orange properties is 0.05, or 1 in 20. This does not mean that buying and developing the orange properties will bankrupt your opponent automatically - the greens obviously have more "killing power" per land. However, they get landed upon so infrequently and are so expensive to develop, you hurt yourself far more than your opponent.

6 comments:
Absolutely epic.
I read something similar to this online a few months ago, but nowhere near this in depth.
This obviously proves the awesomeness of orange.
Orange, oh orange!
Wow, this is awesome. Although I kind of zoned out in the middle, the graphs were pretty. And you should now refer to Kate as "wife", not fiance (even if she was just fiance at the time)
Good analysis. Growing up in a family of eight before video games were invented meant that Monopoly was predominantly a contact sport only slightly less vicious than mixed martial arts with machetes with property trades that would have made an arab bazaar merchant retire his sandals and weep into his tea for the rest of his days.
In such an environment I long ago realized the orange were the best properties, and (something your graphs also point out) that the best ROI for rent is at the three house level for every property. Something to consider when you have to decide whether to invest or save for a rainy day.
I must mention also that cheating in our family took on an art form. If you were caught in the till by another player, it usually meant you had to steal another $500just to shut them up. In one memorable game, my brother was photographed holding the bank to the ceiling while he rolled - it was the only way to discourage stealing so he could concentrate on his turn.
Don't even ask how our Risk, Diplomacy and Kingmaker games were played.
Sullivan013
Now I'm completely convinced that you did go to engineering school... =)
Post a Comment